Questões de trigonometria
Questões de trigonometria
1ª dica: Assista aos vídeos de solução das questões n°3 e n°7
2ª dica: Catetos são os lados do triângulo que formam o ângulo reto.
3ª dica: cateto adjacente é o que está ao lado do ângulo.
4ª dica:
$$sen \alpha =\frac{cateto.oposto}{hipotenusa}$$
$$cos \alpha =\frac{cateto.adjacente}{hipotenusa}$$
$$tg \alpha =\frac{cateto.oposto}{cateto.adjacente}$$
1. Um ciclista sobe, em linha reta, uma rampa com inclinação de 3 graus a uma velocidade constante de 4 metros por segundo. A altura do topo da rampa em relação ao ponto de partida é 30 m.
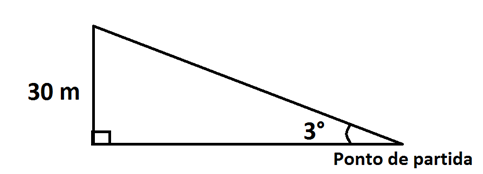
Use a aproximação sen 3° = 0,05 e responda: O tempo, em minutos, que o ciclista levou para percorrer completamente a rampa é:
a) 2,5. b) 7,5. c) 10. d) 15. e) 30.
2. Uma escada, representada na figura pelo segmento AC, mede e está apoiada no ponto C de uma parede, fazendo, com o solo plano, um ângulo tal que $$tg(\alpha) = 2.$$ Uma pessoa que subiu dessa escada está a uma altura, em relação ao solo igual, em u.c. a:

$$a)\frac{\sqrt{2}}{3}$$
$$b)\frac{\sqrt{5}}{2}$$
$$c)\frac{4\sqrt{2}}{3}$$
$$d)\frac{4\sqrt{3}}{3}$$
$$d)\frac{3\sqrt{5}}{2}$$
3. A figura abaixo representa uma pipa simétrica em relação ao segmento AB, onde AB = 80 cm. Então a área da pipa, em m2, é de:
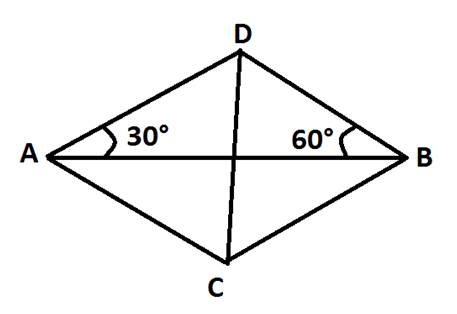
$$a) 8\sqrt{3}$$
$$b) 0,16\sqrt{3}$$
$$c) 0,32\sqrt{3}$$
$$d) 1,6\sqrt{3}$$
$$e) 3,2\sqrt{3}$$
4. Na figura, o segmento é tangente à circunferência de centro C e raio 4 cm e é perpendicular a .
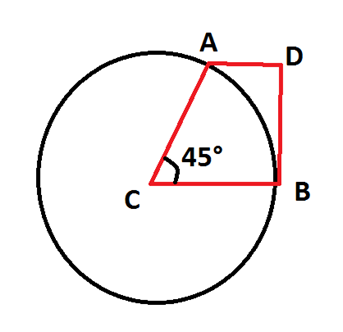
Nessas condições, a área do trapézio ADBC mede, em cm2, aproximadamente:
$$a) 2\sqrt{2}-1$$
$$b) 4\left ( 2\sqrt{2}-1 \right )$$
$$c) 8\sqrt{2}-1$$
$$d) 4\sqrt{2}-1$$
$$e) \sqrt{2}-1$$
5. Em relação ao triângulo ABC abaixo:

Dados AB = 3 cm, AC = 8 cm e  = 60º. Pode-se dizer então, que é verdadeira a seguinte afirmação:
a) Seu perímetro é 20 cm.
$$b) sen A=\frac{1}{2}$$
$$c) sua área é 6\sqrt{3} cm^{2}$$
d) É um triângulo retângulo.
$$e) BH=\frac{7\sqrt{3}}{2}$$
6. O piloto de um pequeno avião, pensando que estava em direção a uma cidade B, ao norte, distante 60 km de seu ponto de partida, equivocou-se em sua orientação e rumou ao oeste. Ao perceber o grave erro cometido, ele corrigiu a rota, fazendo um giro de 120º à direita em um determinado ponto C de sua trajetória, de modo que o seu trajeto, juntamente com o que deveria ter sido seguido, forma um triângulo ABC, retângulo em
A, onde A representa o seu ponto de partida. Com base nessas informações, a distância em quilômetros que o piloto voou, partindo de A até chegar ao ponto B, é:
$$a) 20\sqrt{3}$$
$$b) 60\sqrt{3}$$
$$c) 20+20\sqrt{3}$$
$$d) \frac{70\sqrt{3}}{3}$$
$$e) \frac{20+20\sqrt{3}}{3}$$
7. Paulo fabricou uma bicicleta, tendo rodas de tamanhos distintos, com o raio da roda maior (dianteira) medindo 3 dm, o raio da roda menor medindo 2 dm e a distância entre os centros A e B das rodas sendo 7 dm. As rodas da bicicleta, ao serem apoiadas no solo
horizontal, podem ser representadas no plano (desprezando-se os pneus) como duas circunferências, de centros A e B, que tangenciam a reta r nos pontos P e Q, como indicado na figura.
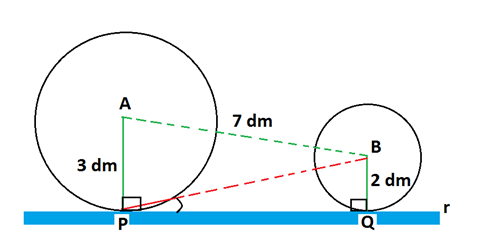
a) Determine a distância entre os pontos de tangência P e Q e o valor do seno do ângulo BPQ.
b) Quando a bicicleta avança, supondo que não haja deslizamento, se os raios da roda maior descrevem um ângulo de 60°, determine a medida, em graus, do ângulo descrito pelos raios da roda menor. Calcule, também, quantas voltas terá dado a roda menor quando a maior tiver rodado 80 voltas.
8. Num triângulo retângulo, a hipotenusa mede 15 e o ângulo AABC mede 60°. A soma das medidas dos catetos vale:
$$a) \frac{15\left ( 1+\sqrt{3} \right )}{4}$$
$$b) \frac{15}{4}$$
$$c) 15\left ( 1+\sqrt{3} \right )$$
$$d) \frac{15}{2}$$
$$e) \frac{15\left ( 1+\sqrt{3} \right )}{2}$$
9. Sobre uma rampa de inclinação constante, que tem 6 m de altura na sua parte mais alta, uma pessoa notou que, após caminhar 15 m, estava a 1,5 m de altura em relação ao solo, conforme mostra a figura abaixo. Nessas condições, a distância que essa pessoa ainda terá de caminhar para chegar ao ponto mais alto dessa rampa é igual a:
a) 30 m b) 35 m c) 38 m d) 40 m e) 45 m

10. Os vértices de um triângulo ABC, no plano cartesiano, são: $$A = (1, 0), B = (0, 1) e C = (0, \sqrt{3}).$$ Então, o ângulo BÂC mede:
a) 60° b) 45° c) 30° d) 18° e) 15°
11. Se, no esquema representado na figura abaixo, as retas I, II e III são paralelas, AB =5 mm, BC = 30 mm e DF = 0,12 m, então calcule o valor de DE.

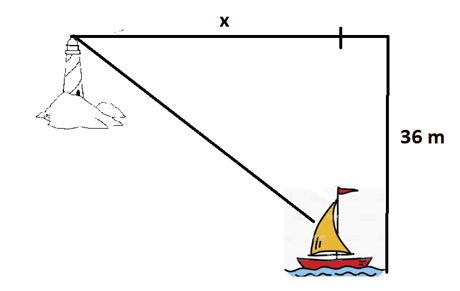
12. Um farol localizado 36 m acima do nível do mar é avistado por um barco a uma distância x da base do farol, a partir de um ângulo. Admitindo-se que $$sen \alpha =\frac{3}{5}$$ calcular a distância x. conforme a figura:
13. Na figura, $$\alpha =\beta $$ AC = 10, BD = 21 e DC = x.
Na figura II, MN // OP. Então a área da figura II é, em unidade de área, igual a:
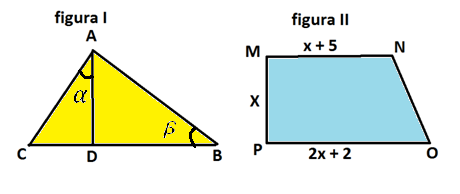
a) 24 b) 38 c) 42 d) 55
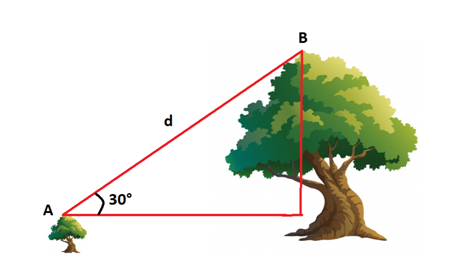
14. Numa floresta as alturas em que estão os topos de duas árvores, A e B, são respectivamente 12 m e 18 m. Do ponto A vê-se o ponto B sob um ângulo de 30° com relação ao plano horizontal. Dados: sen 30° = 0,50, cos 30 = 0,87 e tg = 30° 0,57. A distância d entre os topos das árvores.
a) 6 m b) 8 m c) 12 m d) 18 m e) 24 m
15. Um avião decola de um ponto B sob inclinação constante de 15° com a horizontal. A 2 km de B se encontra a projeção vertical C do ponto mais alto D de uma serra de 600 m de altura, conforme a figura.

Dados: cos 15° = 0,97, sen 15° = 0,26, tg 15° = 0,27. É correto afirmar:
a) não haverá colisão do avião com a serra.
b) haverá colisão do avião com a serra antes de alcançar 540 m de altura.
c) haverá colisão do avião com a serra em D.
d) se o avião decolar 220 m antes de B, mantendo a mesma inclinação, não haverá colisão do avião com a serra.
16. No $$\Delta ABC$$, CF = 20 cm e BC = 60 cm. Assinale as medidas dos segmentos AF e BE respectivamente.
a) 5, 15 b) 10, 20 c) 15, 25 d) 20, 10 e) 10, 5
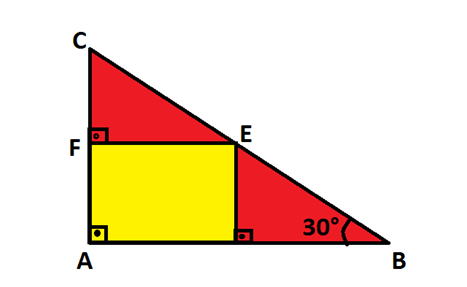
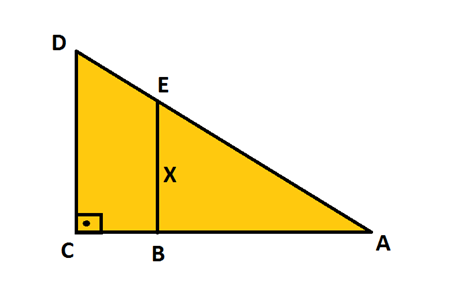
17. Dada a figura abaixo, se AB = 8 cm, CD = 4 cm e AD = 20 cm, a medida, em cm, de x é:
$$a)\frac{\sqrt{6}}{6}$$
$$a)\frac{\sqrt{6}}{2}$$
$$c) \frac{2\sqrt{6}}{3}$$
$$d)\frac{3\sqrt{6}}{2}$$
$$e)\frac{3\sqrt{3}}{2}$$
18. 10. Um marceneiro deseja construir uma escada trapezoidal com 5 degraus, de maneira que o mais baixo e o mais alto tenham larguras respectivamente iguais a 60 cm e a 30 cm, conforme a figura:
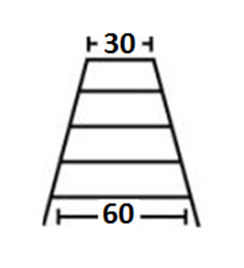
Os degraus serão obtidos cortando-se uma peça linear de madeira cujo comprimento mínimo, em cm, deve ser:
(A) 144. (B) 180. (C) 210. (D) 225. (E) 240.
Gabarito:
1. A
2. C
3. B
4. B
5. C
6. B
7. a) $$\frac{\sqrt{13}}{13}$$
b) 90° e 120 voltas
8.E
9. E
10. E
11. 1,7 m
12. 48 m
13. B
14. C
15. B
16. B
17. C

There is a bonzer contrive item of your team. cursodematematicaonline.com
This website is mostly a stroll-by means of for all the data you needed about this and didn’t know who to ask. Glimpse right here, and you’ll undoubtedly discover it.